PPM Accuracy Calculator

Check how accurate your meter is compared to a calibration solution.

1️⃣ Measurement Data

Known Standard (PPM) True concentration from calibration bottle.

Meter Reading (PPM) Displayed value on your meter.

Acceptable Error (%) 2% is standard for most meters.

Purpose:
Compares your meter reading to a known standard. Formula: Error (%) = |Measured − Known| ÷ Known × 100

Tip: If deviation exceeds tolerance, clean probes and recalibrate using fresh standard solution.

Easy PPM Accuracy Calculator – Find Error in Parts Per Million

A simple tool that converts measurement error into PPM. Great for students, technicians, and beginners needing fast accuracy and tolerance calculations.

In fields that demand high precision—from electronics and chemistry to manufacturing—accuracy isn’t just a goal; it’s a necessity. But how do we measure and communicate this level of accuracy in a standardized way? One of the most common methods is “parts per million,” or PPM. It gives us a clear, scalable way to understand the tiny deviations between an expected value and an actual measured value.

Our PPM Accuracy Calculator is a simple tool designed to do this calculation for you instantly. But to truly appreciate its utility, it’s important to understand what PPM is, how the formula works, and where it’s applied in the real world. This guide will walk you through everything you need to know.

How to Use the PPM Accuracy Calculator

Our calculator is designed for simplicity and speed. In just a few steps, you can determine the PPM error of any measurement.

Step-by-Step Instructions

Enter the Measured Value: This is the actual value you observed or measured with your equipment. For example, if you tested a component and it read 10.005 MHz, you would enter 10.005.
Enter the True Value: This is the ideal, expected, or specified value. It’s the benchmark you’re comparing against. Following the example above, if the component was supposed to be 10 MHz, you would enter 10.
Select the Unit: Choose the appropriate unit (Hz, kHz, MHz, GHz) from the dropdown menu. While the PPM calculation itself is a ratio and technically unitless (as long as the units for both values are the same), this feature helps keep your calculations clear and organized, especially when dealing with frequency. The calculator ensures the math is consistent.
Click “Calculate”: The tool will instantly process the numbers and display the accuracy deviation in parts per million (PPM).

The result shows you exactly how much your measured value deviates from the true value, scaled to a million units.

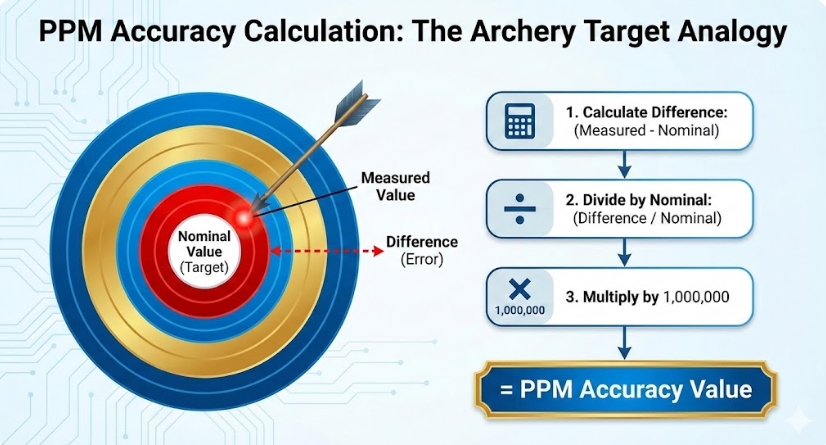
The PPM Formula & Conversion Explained

Understanding the math behind the calculation can help you appreciate what the numbers truly mean. The concept is straightforward: it’s about finding the fractional difference between two values and then scaling it up to be out of one million.

The Core Formula

The formula used by the PPM Accuracy Calculator is: PPM = (Measured Value – True Value / True Value) * 1,000,000

Let’s break this down:

|Measured Value – True Value|: First, we find the difference between your measurement and the ideal value. We use the absolute value (indicated by the | | bars) because we only care about the magnitude of the error, not whether it was higher or lower. An error is an error, regardless of its direction.
(… / True Value): Next, we divide that difference by the true value. This turns the absolute error into a fractional or relative error. This step is crucial because it puts the error into context. For example, an error of 1 is very significant if your true value is 10, but almost negligible if your true value is 10,000.
* 1,000,000: Finally, we multiply this fraction by one million. This scales the result to express it in “parts per million.” It makes it easier to read and compare very small error values that would otherwise be long decimal numbers.

A Practical Example

Let’s say you’re working with a crystal oscillator that is specified to have a frequency of 25 MHz (the True Value). You use a frequency counter and measure its actual output to be 25.0003 MHz (the Measured Value).

Let’s plug this into the formula:

Calculate the difference: |25.0003 – 25| = 0.0003
Divide by the true value: 0.0003 / 25 = 0.000012
Multiply by one million: 0.000012 * 1,000,000 = 12 PPM

The result, 12 PPM, tells us that for every million cycles the oscillator is supposed to produce, it actually produces an extra 12. This is a much more intuitive way to express the error than saying it has a fractional error of 0.000012.

Applications & Use Cases of PPM Accuracy

PPM is not just an abstract mathematical concept; it’s a critical metric used across numerous industries to ensure quality, safety, and performance.

Electronics and Engineering

This is one of the most common fields where PPM is used. The stability and reliability of electronic devices often depend on the precision of their individual components.

Crystal Oscillators: As seen in our example, these time-keeping components are rated in PPM. A lower PPM value means a more stable clock, which is critical for computers, communication systems, and watches.
Resistors: The tolerance of a resistor, which indicates how much its actual resistance can vary from its stated value, is often expressed in PPM per degree Celsius (PPM/°C). This tells you how much the resistance will drift as the temperature changes.
Voltage References: In circuits that need a very stable and precise voltage, the voltage reference component will have its stability rated in PPM/°C.

Did you visit our PPM calculator?

Chemistry and Environmental Science

In chemistry, PPM is used to denote the concentration of a substance within a solution or mixture.

Water Quality: The concentration of minerals, contaminants (like lead or mercury), or added substances (like fluoride) in drinking water is measured in PPM.
Air Quality: Pollutant levels, such as carbon monoxide (CO) or nitrogen oxides (NOx) in the air, are monitored and reported in PPM. This helps environmental agencies assess public health risks.
Chemical Purity: When manufacturing chemicals, PPM is used to specify the maximum allowable level of impurities.

Manufacturing and Quality Control

PPM is a key performance indicator (KPI) in quality control, especially in mass production environments like automotive or electronics manufacturing.

Defect Rate: Instead of saying a process has a 99.99% success rate, a manufacturer might aim for a defect rate below 100 PPM. This means for every million parts produced, fewer than 100 are defective. This is a core concept in methodologies like Six Sigma, which aims for as low as 3.4 defective parts per million opportunities.

Frequently Asked Questions (FAQs)

1. What exactly is PPM and why is it important for accuracy?

Parts per million (PPM) is a way of expressing a very small concentration or error. It’s a dimensionless quantity that represents one part in a total of one million parts. It’s important because it provides a universal, standardized scale to compare the accuracy of different measurements, components, or systems, regardless of their original units or magnitude.

2. Is a higher or lower PPM value better?

A lower PPM value is always better. A lower number signifies a smaller deviation from the true or ideal value, meaning the measurement or component is more accurate and has less error. For example, a 10 PPM oscillator is more stable and precise than a 50 PPM oscillator.

3. What’s the difference between PPM and percentage error?

Both measure relative error, but they use different scales. Percentage error is parts per hundred (%), while PPM is parts per million. The conversion is straightforward:

1% = 10,000 PPM

PPM is preferred when dealing with very small errors because the numbers are more manageable. An error of 0.0025% is the same as 25 PPM. For most people, “25 PPM” is easier to understand and compare than “0.0025%”.

4. Can I use the PPM Accuracy Calculator for any unit?

Yes, as long as the Measured Value and True Value are in the same unit. The formula is a ratio, so the units cancel each other out. You could use it to compare grams, meters, seconds, or volts. Our calculator includes a unit selector for frequency (Hz, kHz, etc.) as this is a very common application, but the mathematical principle is universal.

5. How accurate is “good enough”? What’s a typical PPM value?

This depends entirely on the application.

For a simple hobbyist electronic project, a resistor with a tolerance of 5% (50,000 PPM) might be perfectly fine.
For a standard computer or smartphone, a crystal oscillator might have a stability of 20-50 PPM.
For high-end scientific or telecommunications equipment, components might require accuracy of 1 PPM or even lower (often expressed in parts per billion, or PPB).

6. What does a negative PPM value mean?

In the standard formula, you won’t get a negative PPM value because we use the absolute difference between the measured and true values. The PPM figure represents the magnitude of the error, not its direction (i.e., whether the measured value was higher or lower than the true value). The goal is simply to quantify the size of the deviation.

7. Why do we multiply by 1,000,000?

We multiply by one million to convert the tiny fractional error into a more readable whole number. For instance, a fractional error of 0.000012 is small and cumbersome. Multiplying it by 1,000,000 gives us “12,” and we simply add the “PPM” label to give that number its context. It’s purely for convenience and standardization.